Trước hết ta điểm qua các máy tính, phần mềm, trang web đã tính "0 mũ 0" như thế nào?
Đầu tiên là Google. Công cụ tính toán của Google đã cho rằng: $0^0=1.$
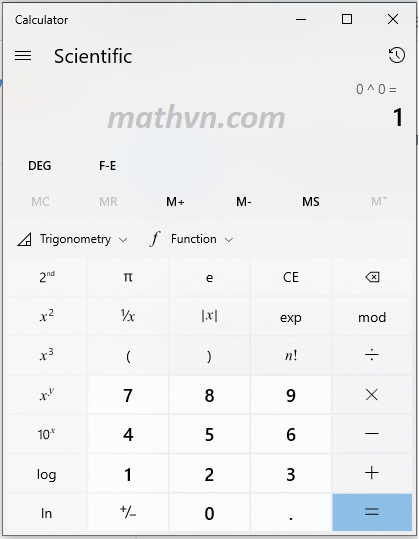
Tiếp theo là phần mềm Calculator cài sẵn trong hệ điều hành Windows trên máy tính, kết quả vẫn là $0^0=1.$
Một trang web nổi tiếng về tính toán và vẽ đồ thị là Desmos cũng cho kết quả là: $0^0=1.$
Hầu hết các máy tính cài sẵn trên smartphone cũng cho kết quả như vậy. Hai phần mềm toán học chuyên dụng là Maple và Mathlab cũng cho ra $0^0=1.$
Vậy có phải "0 mũ 0 bằng 1"?
1. $0^0=1$
Có một số lập luận đã chỉ ra rằng $0^0=1. \ \ \ \ $ Sau đây là 2 trong số các lập luận đó.Lập luận 1
Khảo sát và vẽ đồ thị hai hàm số $y=x^x \ \ \ \ $ và $y=(\sin x)^x \ \ \ \ $, ta được kết quả trong 2 hình sau:
 |
| Đồ thị hàm số y=x^x |
 |
| Đồ thị hàm số y=(sin x)^x |
$$\lim_{x \to 0^+}x^x=1 \ \ \ \text{và} \ \ \ \lim_{x \to 0^+}(\sin x)^x=1$$
Lập luận 2
Từ định lí khai triển nhị thức Newton:
$$(a+b)^n = \sum\limits_{k=0}^n C_n^k a^{n-k}b^k$$
Áp dụng cho $a=1, b=0$ ta được:
$$1=(1+0)^n= C_n^0.0^0 + C_n^1.0^1 + C_n^2.0^2 + ... + C_n^n.0^n$$
Để đẳng thức này đúng thì phải thừa nhận $0^0=1.$
2. $0^0 \ \ \ \ $ là một dạng vô định
Một trang web tính toán nổi tiếng khác là Wolfram Alpha thì cho rằng $0^0 \ \ \ \ $ là một dạng vô định. |
| Kết quả tính 0^0 từ Wolfram |
Ở phần 1, ta có hai giới hạn dạng $0^0 \ \ \ \ $ và đều tính ra bằng $1.$ Tuy nhiên, không phải mọi giới hạn dạng $0^0 \ \ \ \ $ đều có kết quả như vậy. Chẳng hạn:
$$\lim\limits_{t \to 0^+} \left( {e^{-1/t^2}} \right)^t = 0 \\ \lim\limits_{t \to 0^+} \left( {e^{-1/t^2}} \right)^{-t} = +\infty \\ \lim\limits_{t \to 0^+} \left( e^{-t} \right)^{2t} = e^{-2}$$
Ngoài ra, nếu xét hàm hai biến $f(x,y)=x^y \ \ \ \ $ thì hàm số này không tồn tại giới hạn khi $(x,y) \to (0,0).$
Như vậy $0^0 \ \ \ \ $ lại là một dạng vô định.
3. Tóm lại
Chính vì những lý do trên nên đã có những sự khác biệt giữa các phần mềm, trang web tính toán nổi tiếng như đã đề cập ở mục 1 và mục 2. Trong hầu hết giáo trình và sách Toán học, người ta xem $0^0 \ \ \ \ $ là dạng vô định nhưng có một số giáo trình khác lại quy ước $0^0 = 1.$Tham khảo ThuNhan, Wolfram, Desmos. Người đăng: MiR Math.